3-D Printing -- Project #2

For our second 3-D design project, I had students make game tokens for games they were designing.   They have been using systems of inequalities in 3-variables along with Mathematica to design and print 3-D objects.  There are no shortcuts -- everything is defined by an equation.

I told them that one of my regrets as a parent is that I didn't have my children (who are now out of college) mathematically design and 3-D print their own game pieces that they could carry with them wherever they went.  That way, while other kids could fight about who was going to be the race car and who had to be the thimble, my well-prepared children could pull out a personalized way-cool game token and say, "I'm good."  Ah, opportunity lost.

We began by learning about the equations to circles, and I gave them some challenges to complete -- create a cylinder, intersecting cylinders, a cylinder with a hole, and the car-looking-thing below.

 
 

Most were successful pretty quickly, as they'd become used to thinking in more than just the x-y axis from our previous work in Mathematica.

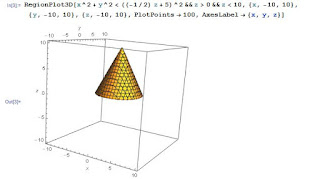
The next set of challenges were more difficult.  I had them think about how a cone and a cylinder are related.  They could see that a cone is a cylinder whose radius changes as you move "up."  That is, if the cylinder has its base in the x-y plane, the radius of the cone changes as z changes -- r is a function of z.

For example, if we want our cone to have a base radius of 5 and a height of 10, we take the inequality of the cylinder:

x^2 + y^2 < 5^2

and replace the radius (5) with a function of z.  When z = 0, r = 5 and when  z = 10, r = 0.  We're really looking for the equation to the line between these two points, which is r = -1/2 z +5.

So, the new inequality for the cone is:

x^2 +y^2 < (-1/2 z + 5)^2

Many mathematical tangents to talk about here. 

• How would we write the equation to a cone with the relevant variables (Height, base radius, and center of base)?
• We've used composition of functions in a productive way.
• What if we wanted the sides to be a parabola, for example, or a Hershey's kiss?  This would lead us to fitting quadratics and higher degree polynomials to data.
• How would we think of a (hemi-)sphere this same way, and develop the formula for a sphere?

Two further challenges followed.  The rocket ship reviewed how to place two objects in one design.  The leaning tower keeps the radius constant, but makes the x-coordinate of the center a function of z.

 


Again, many more paths to pursue.  In particular, what would happen if both the x and y coordinates were functions of z?  What if they were different functions, say a quadratic and a line?  We're hinting toward parametric functions here and are also begging for periodic functions, neither of which we've covered yet.  Maybe next year I'll rearrange things.

The only requirements for the game piece was that it had to have at least one quadratic, at least one circle and at least one changing dimension (like the cone).  The results were varied and excellent.  Some students were pretty literal and made actual game pieces, with appropriate detail.  Some were abstract, and others were representational.  Particularly impressive was Jake's dragon, which used around 200 inequalities, including lines, parabolas, circles, spheres and a very cool third-degree polynomial neck.  (Photos of a sampling the student work are below.)

Once again, I heard all the good classroom sounds, particularly frustration turned through persistence into joy.  Music to my ears.

Next year, I will rearrange some things so that we can be more creative in our "changing radius" possibilities.  I'm considering, too, adding in some parametric graphing which will open up new possibilities as well.  That's another thing on my list to think about this summer.